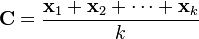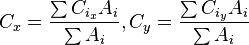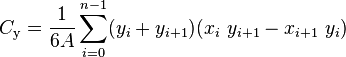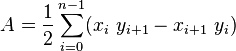algorithmic modeling for Rhino
Hello,
I don't know if this is intentional, but it sure is confusing. The [Polygon Center] component computes the center as the mean of all the vertices in a polygon. According to Wikipedia, it equals this:
The centroid of a finite set of
points
in
is
However the center of a polygon by decomposition is this.
The centroid of a plane figure
can be computed by dividing it into a finite number of simpler figures
, computing the centroid
and area
of each part, and then computing
Or this in general:
The centroid of a non-self-intersecting closed polygon defined by n vertices (x0,y0), (x1,y1), ..., (xn−1,yn−1) is the point (Cx, Cy), where
and where A is the polygon's signed area,
Shouldn't the [Polygon Center] use this formula instead, or clarify that the "center" given is the mean?
EDIT: Sorry to have posted this in VB, C# and Python Coding. I meant to post it in Errors, Bugs and Oversights.
Views: 8128
- Attachments:
Replies to This Discussion
-
Just for triangles there are literally thousands of possible definitions for what is meant by the center.
I'm not exaggerating - check out this encyclopedia of triangle centers !
While there probably aren't quite so many that apply to general polygons, there are still a lot of possibilities :)
-
-
Great example of how a simple idea can get complicated :D
-
-
Polygon center computes two different centroids. Vertex average (which is admittedly a terrible way to define a center, as the shape of a polygon doesn't really matter much) and Edge average (which is a lot better and also the only result you actually see the preview of).
I can certainly add more algorithms as long as they're quick to compute. Any suggestion (source or pseudo code please, no mathematical argle-bargle, can't read that) on which one you'd like to see?
--
David Rutten
david@mcneel.com
Tirol, Austria
-
-
Well I wasn't looking for it to be included, but now that you say so the code is actually on stackoverflow :).
My point was that the component's name is a bit confusing, since what the component returns in [Cv] is not a polygon's center, but the center of a set of points. ([Ce] I still don't understand very well what it returns).
-
-
I tested the Area centroid algorithm. It gives the same point you would have gotten with the Area component of course, but it does do it somewhat quicker. This new centroid algorithm can't handle non-planar polygons though, but I suppose that's not an issue?
--
David Rutten
david@mcneel.com
Tirol, Austria
-
-
Hey David,
I'm not sure we are in the same page. The code from the link I posted computes the centroid of a polygon (planar by definition). I think it would make most sense to add it to the [Polygon Center] component. Naming it Area centroid might be confusing...
I'm curious as to what happens if you input a intersecting planar curve in it. Should it give the correct centroid of the curve, maybe you could name it planar curve centroid or something to your better judgment.
-
-
We're on the same page, but my problem is that it won't work on non-planar polygons. The current component does. So if I create a new component which also computes the area centroid, does it turn orange when you provide a non-closed and/or non-planar polygon? If so, that's sort of annoying. If not, how do I communicate to the user that one of the outputs doesn't exist because the polygon is non-planar?
--
David Rutten
david@mcneel.com
Tirol, Austria
-
-
The current [area centroid] works on non-planar curves? Are you talking about the left one or right one?
For me only the right one works on non-planar curves. The left one wont. But maybe it's because I'm on 0.90014.
Well I'm done for today. Maybe it's best you leave it all as is. But the polygon's center component's name is a bit confusing ;)
Best
-
-
I see we were talking about the same thing. You had me confused when talking about the Area centroid; thought you meant the [Area] component.
That could be a solution. Another (probably messy) solution could be to rename the existing [Polygon Center] component to [Curve Center], and use the new algorithm exclusively for the [Polygon Center] component.
Since polygons are by definition planar, there would be no ambiguity with the component. And the existing [Cv] and [Ce] which strictly speaking don't apply do polygons would be used on curves. But you'd have to overhaul the existing [Polygon Center] component and I'm sure that would cause some pretty messy problems.
Finally another solution could be to use the new algorithm on a new [Planar Polygon Center] component, and leave the existing one as is, or maybe change it's image/description.
David, what happens with the new algorithm is the polygon is self-intersecting?
-
-
Does this not defeat the object of why this particular component was born?
When trying to find the centre of a "regular" cell, we were using the Area component to calculate the Area Centroid which was proving to be very slow.
Thus a mathematical efficient method was needed hence this component.
Please do not include the Area calculation.
-
-
Maybe for non-planar polygons it could triangulate them, then combine the area weighted triangle centroids?
-
© 2025 Created by Scott Davidson.
Powered by
![]()