working with ratios

I'm currently working on a definition where I will like to work with a division of a line in a ratio 2:1, is there a different way of doing it from a plain 3 part division? I will like to be able to situate a point at this place, which will be very different from situating it at 1:2 position.

Replies to This Discussion

Permalink Reply by Armin Seltz on September 26, 2016 at 10:39am

Hmm, not sure what you are trying to do. You should include a small drawing when you dont have a grasshopper file yet.

But it sounds like you want to get the point on a curve along it. That is called the "Parameter" and it is used in Grasshopper a lot. If you for example use the "Evaluate Curve" component it will ask for a curve and a parameter at which to evaluate the curve.

Normally the parameter is dependent on the length of the curve and NOT linear! What you can do is to "reparametrize" a curve, where you basically say that no matter how long the curve, the parameters should go from 0 to 1, where 0 is the start of the curve and 1 is the end.

So then you can do exact ratios or points on curves, independent of their length. To reparametrize a curve, you can either use that function by right-clicking on a curve input or using the component.

Permalink Reply by David Rutten on September 27, 2016 at 3:21am

Normally the parameter is dependent on the length of the curve and NOT linear! What you can do is to "reparametrize" a curve, where you basically say that no matter how long the curve, the parameters should go from 0 to 1, where 0 is the start of the curve and 1 is the end.

Reparameterizing will not make the parameterization linear, it will merely make it go from zero to one. If you want a point/parameter at some specific ratio along the length of the curve, you must use [Evaluate Length].

Permalink Reply by Armin Seltz on September 27, 2016 at 4:54am

Yes, I notice now that wasn't really clear. I didnt say it does, but should have emphasized that it doesn't.

Also you can rebuild a curve to make parameters linear, but have to be careful to use enough points. The curve will always just be an approximation and get closer to the original the more points you add.

Permalink Reply by David Rutten on September 27, 2016 at 5:09am

Also you can rebuild a curve to make parameters linear, but have to be careful to use enough points.

Sorry, not true either. Only lines and circles/arcs* are guaranteed to have linear parameterization. Nurbs curves are almost never linear. It is true that rebuilding a curve may reduce the discrepancies between parameters and length progression, and indeed the more points you use the more linear it'll become, but especially non-periodic curves will usually have a 'stretched' parameter space near the ends where the curve is clamped to the first and last control-point.

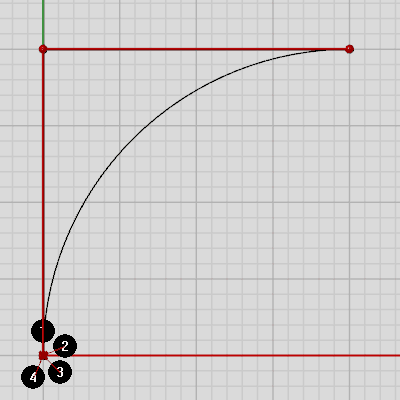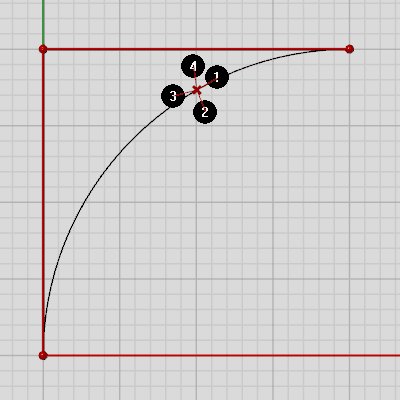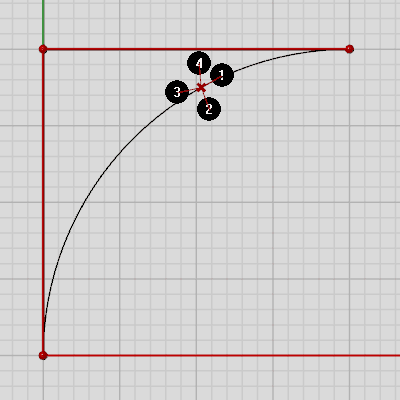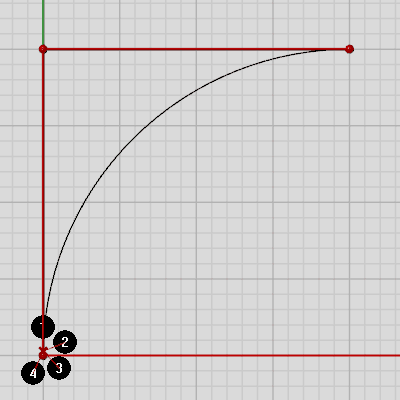
Note how the first, second, third and fourth derivatives of a genuine arc are constant while sampling along it, while a nurbs curve with the same shape has different derivatives:

* genuine circles and arcs, degree=2 nurbs curves that approximate circles and arcs do not, see this blog post.

Permalink Reply by Armin Seltz on September 27, 2016 at 6:02am

Ok, I stand corrected. Very interesting and good to know!

Great article in the blog by the way and love the addendum, where you compare parameters to trip times along various roads.

You say that evaluating a curve at a certain length is much more calculation intense as at a parameter, which makes sense. Can you tell us what factors we are talking about here? How does it work? Is it an iterative process?

Permalink Reply by David Rutten on September 27, 2016 at 8:15am

Can you tell us what factors we are talking about here? How does it work? Is it an iterative process?

Ouch... we're rapidly approaching the limit of my knowledge here. I can tell you it is an iterative process, analytic solutions are not possible for Nurbs curves*. They are possible for polylines and (I think) conics, but I'm not sure if the latter is special cased in Rhino.

There's a lot of research on this but I have no idea what algorithm specifically has been implemented in Rhino. However I feel pretty confident in saying that considering the fundamental importance of arc-length parameterizations whatever the implementation is, it is robust and heavily optimized.

* If you're surprised by this, consider that nobody knows how to correctly calculate the length of an ellipse. Only approximate methods are known.

Permalink Reply by David Rutten on September 27, 2016 at 8:56am

By iterative I meant that the curve is broken up into small pieces, each of which can be solved to well within tolerance, then they are put back together. The sum-total of all pieces equals the total length of the curve, and once this table of piece-lengths exists it can be used to speed up other length-based calculations.

I suspect the pieces are solved using the integrals of the nurbs equations, that seems to be the method all online descriptions of algorithm use.

Permalink Reply by Armin Seltz on September 27, 2016 at 8:59am

Right. Okay, thats really interesting. Thanks for always taking the time to explaine things so well :)

Permalink Reply by ng5 Alex on September 27, 2016 at 6:13am