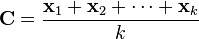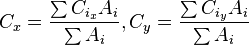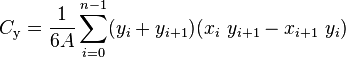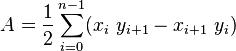algorithmic modeling for Rhino
Hello,
I don't know if this is intentional, but it sure is confusing. The [Polygon Center] component computes the center as the mean of all the vertices in a polygon. According to Wikipedia, it equals this:
The centroid of a finite set of
points
in
is
However the center of a polygon by decomposition is this.
The centroid of a plane figure
can be computed by dividing it into a finite number of simpler figures
, computing the centroid
and area
of each part, and then computing
Or this in general:
The centroid of a non-self-intersecting closed polygon defined by n vertices (x0,y0), (x1,y1), ..., (xn−1,yn−1) is the point (Cx, Cy), where
and where A is the polygon's signed area,
Shouldn't the [Polygon Center] use this formula instead, or clarify that the "center" given is the mean?
EDIT: Sorry to have posted this in VB, C# and Python Coding. I meant to post it in Errors, Bugs and Oversights.
Views: 7958
- Attachments:
Replies to This Discussion
-
But triangulation is not obvious either, there are typically more ways than one to triangulate a polygon with more than three edges. At that point there would be just as much variability in the possible triangulated-centroid answers as there is now between the area-centroid and the edges-average.
--
David Rutten
david@mcneel.com
Tirol, Austria
-
-
Triangulating the curve is what I did in the definition. But David is right, there is no unique way of triangulating a (3d) curve. I'd say (not 100% sure) that only in polygons (planar) do all unique triangulations collapse at the same point.
You could apply the delaunay triangulation, but this selection is completely arbitrary. Plus you'd be duplicating functions in grasshopper.
-
-
but for planar polygons, all possible triangulations will give the same result when combining their area weighted centroids into one, so it shouldn't matter which one we choose.
For nearly planar polygons different triangulations will give nearly identical results. If it's not even nearly planar, then I don't think the problem is well defined, so surely any answer is pretty meaningless.
-
-
You're right, however triangulation is an expensive method so I hesitate to put it into a component which was quite fast up until now.
There's [Fragment Patch] and [Area] for these complicated fringe cases. Benefit is that you can at least see how the polyline has been triangulated with fragment patch.
--
David Rutten
david@mcneel.com
Tirol, Austria
-
- ‹ Previous
- 1
- 2
- Next ›
© 2024 Created by Scott Davidson.
Powered by
![]()