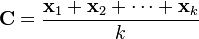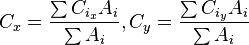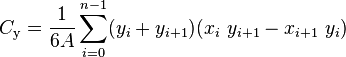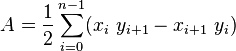Polygon center

Hello,

I don't know if this is intentional, but it sure is confusing. The [Polygon Center] component computes the center as the mean of all the vertices in a polygon. According to Wikipedia, it equals this:

The centroid of a finite set of ${k}$ points $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k$ in $\mathbb{R}^n$ is

$\mathbf{C} = \frac{\mathbf{x}_1+\mathbf{x}_2+\cdots+\mathbf{x}_k}{k}$

However the center of a polygon by decomposition is this.

The centroid of a plane figure $X$ can be computed by dividing it into a finite number of simpler figures $X_1,X_2,\dots,X_n$ , computing the centroid $C_i$ and area $A_i$ of each part, and then computing

$C_x = \frac{\sum C_{i_x} A_i}{\sum A_i} , C_y = \frac{\sum C_{i_y} A_i}{\sum A_i}$

Or this in general:

The centroid of a non-self-intersecting closed polygon defined by n vertices (x₀,y₀), (x₁,y₁), ..., (x_n−1,y_n−1) is the point (C_x, C_y), where

$C_{\mathrm x} = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)$

$C_{\mathrm y} = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)$

and where A is the polygon's signed area,

$A = \frac{1}{2}\sum_{i=0}^{n-1} (x_i\ y_{i+1} - x_{i+1}\ y_i)\;$

Shouldn't the [Polygon Center] use this formula instead, or clarify that the "center" given is the mean?

EDIT: Sorry to have posted this in VB, C# and Python Coding. I meant to post it in Errors, Bugs and Oversights.

Attachments:

polygon center.gh, 5 KB

Replies to This Discussion

Permalink Reply by David Rutten on September 23, 2013 at 2:21am

But triangulation is not obvious either, there are typically more ways than one to triangulate a polygon with more than three edges. At that point there would be just as much variability in the possible triangulated-centroid answers as there is now between the area-centroid and the edges-average.

David Rutten

david@mcneel.com

Tirol, Austria

Permalink Reply by Jesus Galvez on September 23, 2013 at 4:47am

Triangulating the curve is what I did in the definition. But David is right, there is no unique way of triangulating a (3d) curve. I'd say (not 100% sure) that only in polygons (planar) do all unique triangulations collapse at the same point.

You could apply the delaunay triangulation, but this selection is completely arbitrary. Plus you'd be duplicating functions in grasshopper.

Permalink Reply by Daniel Piker on September 23, 2013 at 6:29am

but for planar polygons, all possible triangulations will give the same result when combining their area weighted centroids into one, so it shouldn't matter which one we choose.

For nearly planar polygons different triangulations will give nearly identical results. If it's not even nearly planar, then I don't think the problem is well defined, so surely any answer is pretty meaningless.

Permalink Reply by David Rutten on September 23, 2013 at 6:54am

You're right, however triangulation is an expensive method so I hesitate to put it into a component which was quite fast up until now.

There's [Fragment Patch] and [Area] for these complicated fringe cases. Benefit is that you can at least see how the polyline has been triangulated with fragment patch.

David Rutten

david@mcneel.com

Tirol, Austria