algorithmic modeling for Rhino
Gradient Descent
Hi All,
I want to make a Gradient Descent algorithm which iteratively performs small steps in the direction of the negative gradient towards a (local) minimum (like a drop of water on a surface, flowing downwards from a given point in the steepest descent direction). Does anyone know how to do this?
http://en.wikipedia.org/wiki/Gradient_descent
http://www.20sim.com/webhelp/toolboxes/time_domain_toolbox/optimiza...
I want to make a Gradient Descent algorithm which iteratively performs small steps in the direction of the negative gradient towards a (local) minimum (like a drop of water on a surface, flowing downwards from a given point in the steepest descent direction). Does anyone know how to do this?
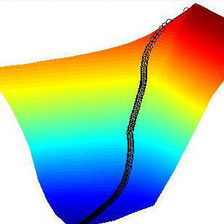
http://en.wikipedia.org/wiki/Gradient_descent
http://www.20sim.com/webhelp/toolboxes/time_domain_toolbox/optimiza...
Views: 11906
Replies to This Discussion
-
Hi Luke,
this is very difficult since the input for every iteration is typically the result of the previous iteration. There is no mechanism for this in Grasshopper itself. Now, since you've posted this on the programming forum I'm guessing you're looking for a VB or C# approach to this?
Here are two algorithms (pseudo code, very similar) which will simulate a droplet of water on a surface (ignoring momentum, surface tension, surface angle, collisions with other drops etc.)
Algorithm one, easy implementation, slows down on horizontalish areas:
1) Pick a point somewhere on the surface. How you get to this level is your problem.
2) Lower the point by a certain fixed amount along the z-axis. Say, 0.1 units.
3) Project the lowered point back onto the BRep using a ClosestPoint function.
4) If the newly projected point is very similar to the input point, abort, otherwise, repeat step 2.
Algorithm two, more difficult, better control over step size:
1) Pick a point somewhere on the surface. How you get to this level is your problem.
2) Find the normal vector at this point.
3) If the normal vector is (nearly) straight up, abort.
4) Find the CrossProduct between the normal vector and the straight-up vector.
5) Rotate the normal vector 90 degrees around this cross-product.
6) Scale the rotated vector so it becomes the length of your sampling accuracy.
7) Move the point along the vector and pull it back onto the surface (should be a short distance if your step-size is small)
--
David Rutten
david@mcneel.com
Poprad, Slovakia -
-
quick version of option 2
-
-
Hello Enrique,
It would be very helpful to see the script for something Im trying to figure out regarding finding a closest path along a topography. Would you mind sharing it?
Thanks,
m
-
-
Hallo
Something to add
You can get the first derivat of a rhino surface with inside a Script block.
This will basicly do what point 2-5 in version two does.
Added a sample script, which is a bit faster then what I got from here
Don't know if that makes sense ...
maeh Schaf - Attachments:
-
-
Hi All
I've used the first bit of option two again for a quick slope mesh viewer, colouring mesh vertex
actually, what i need is some curves at some threshold slope values.
So I rebuilt the mesh changing the values with the slope values, in order to slice it.
the problem is that i'm having real pb to get the curve out of the intersection.
any idea of slicing a mesh?
or another approach to have a slope analysis over a mesh defining regions?
thanks! -
-
Here's my idea for a possible approach to scripting this:
Treat the surface as a 2D scalar field where the value at each point is the height.
For each point find the values of its 4 neighbours (above,below,left,right) some small distance away.
Define a vector for each point in terms of the difference between the value of the point and its neighbours like so:
x= (right-point)+(point-left), y = (above-point)+(point-below)
I think that should give you a vector field which is an approximation to the gradient at each point.
You can then use any of the standard vector field integration techniques to extract your curves. The simplest being Euler's method - just move along the vector from a point, find the new vector at the endpoint, move along that, find the new vector, and so on.
Hopefully with a small enough sample size that should give reasonable results.
Apart from the final integration, you could probably even do that without scripting.
I'm not sure if this is a standard technique, and I've never tried it out in this context, but I used something vaguely similar for a very different purpose in this processing sketch. -
-
Actually, now I think about it, I guess what I describe above is pretty much the same as David's second method. There's no need to take differences between neighbours, just use the surface normal at each point and ignore the z-component to get the vector field. No rotation or cross-products, but you would need to project the lines back onto the surface once they are done.
-
-
Hi Michiel,
Your definition would be very helpful for something im trying to build regarding route planning along a topography. Would you mind sharing it?
Thanks in advance,
M -
-
Hi Michiel,
this definition is very interesting.
Could you share your definition, I'm really curious!!
Mirco
-
-
The result looks great:)
I added randomness to the insertion points in my script. It helps greatly on the visual result. I'll send you the script if you are interested.
-Jørgen -
-
Ah, here we are again :)
I trimmed down the scritp to only include the random distribution. Each point is positioned randomly within it's separate square.
Dim strObject, arrBox, dblX, dblY, strDensity, n, x, y, dblRan1, dblRan2, arrResults
strObject = Rhino.GetObject("Select a surface",8,,True)
If Issurface(strObject) Then
strDensity=1
arrBox=Rhino.boundingbox(strObject)
'-------------------------------- Adding and projecting data
dblX=Round(Rhino.Distance (arrBox(0), arrBox(1)),0)/strDensity
dblY=Round(Rhino.Distance (arrBox(0), arrBox(3)),0)/strDensity
Dim ArrPoints()
n=0
For x=0 To dblX
For y=0 To dblY
Randomize
dblRan1=rnd
Randomize
dblRan2=rnd
ReDim Preserve arrPoints(n)
arrPoints(n) = array((arrbox(0)(0)+x*strDensity)+(dblRan1*strDensity),(arrbox(0)(1)+y*strDensity)+(dblRan2*strDensity),(arrbox(7)(2)+10))
n=n+1
Next
Next
arrResults = Rhino.ProjectPointToSurface(arrPoints, strObject, Array(0,0,-1))
Rhino.addpoints arrResults
End If -
-
Sorry had some errors in the math ....
Here the corrected Script - Attachments:
-
© 2025 Created by Scott Davidson.
Powered by
![]()