algorithmic modeling for Rhino
Hello,
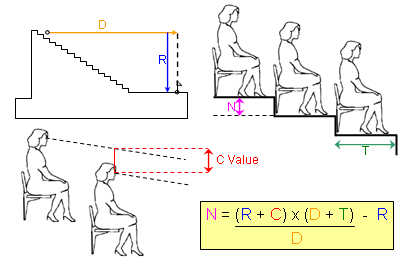
I would like to design on grasshopper the curve of a perfect stadium stand wich is given by this function :
N(k) = ((R+C) x (D+T) / D) - R
With :
R = R0 + sum(R(k-1))
D = D0 + (k-1) x T
With this variable R0 : D0 ; T ; C
I don't succed in entering the function D in the The N(k) function
Could you please help me ?
Views: 1882
- Attachments:
Replies to This Discussion
-
So k is an integer indicating the row and N(k) is the elevation at that point?
-
-
And what exactly does sum(R(k-1)) mean?
-
-
I found this image, sum(R(k-1)) must be sum of N+height of eye or R from row 1 to k-1
http://people.bath.ac.uk/ps281/maths_talk/stadiums/teacher_notes/si...
http://people.bath.ac.uk/ps281/maths_talk/stadiums/teacher_notes/ar...
-
-
The problem with this is that it is not a function in the sense of f(x). It's the definition of a sequence where each number depends on the previous value. As such you cannot simply evaluate this.
Unless you can rewrite this sequence to a f(x) = [x] form, you'll probably end up writing a C# or python script which can loop over the sequence and thus grow it one element at a time.
-
- Attachments:
-
-
Hello Laurent,
It's exactly that thank's a lot, I didn't know the recursive function Anenome.
-
- Attachments:
-
-
If it was me, I would always set/constraint N to the multiplies of a step height(riser)
i.e if a riser height is 15 cm then N will be either 45/60/75 etc
but i am not sure, any one?
-
-
Well ... it's a bit more complex than that since the Z focus of sight has to be considered (a theater and a baseball stadium are not the same) PLUS (a) the max allowed sight distance (b) sight clearance for multi leveled arrangements (c) aisle step design constrains (d) evacuation constrains (e) sight comfort angles ... (z) you name it.
Other than that populating such layouts with something (seats and/or figures) requires - obviously - instance definitions : Imagine 80K seats for example present for some classic master drawing or some photo realistic stuff.
-
© 2024 Created by Scott Davidson.
Powered by
![]()