Point Cloud Optimization

Dear Community,

Let's say I have a random generated point cloud and generate connections using proximity3d. So I get connections with a range of varying random lengths.

Can anybody think of a way to optimize a point cloud to limit the size of these connections to 5 or 10 different lenghts without becoming regular? In order to have a 3d line network consisting of a limited number of line families.

Thanks,

Oliver

Replies to This Discussion

Permalink Reply by Florian Frank on November 9, 2013 at 3:29am

Hi Oliver,

I think this fairly impossible to do with regular operations in GH. Also scripting will get highly recursive and so i decided to make a quick example how this could be done with kangaroo.

CONNECTIONS WITH DIFFERENT LENGTHS

CONNECTIONS WITH EQUILIBRATED LENGTHS (5 different)

It won't be the most precise result with kangaroo but it should give an idea and has a lot of potential for optimization. Since I'm back to IBK you can also walk by the Koje and we can investigate ;-)

Hope this helps. Have a nice weekend,

Attachments:

pointCloud01.gh, 15 KB

Permalink Reply by oliver von Malm on November 11, 2013 at 4:14am

Hi Florian,

Thanks very much for your reply. Actually I tried the same thing before, and basically it is a good idea, but I would actually need more accurate results. In my setup with springs in kangaroo it only got as precise as to the next integer... the thing is, it will have to be something produced 1:1. So not much tolerance. Thinking there might be some global geometrical solution to it, maybe array of possible cominations with given lenths, not sure yet. Some kind of packing/self assembly algorithm. not sure, but any ideas very much appreciated.

Cheers, Oliver

Permalink Reply by Florian Frank on November 11, 2013 at 11:27am

I doubt there is a global geometrical solution to it. Especially, if you like to have the connections to be random and compact, similar to the image above.

This is a classical "wicked problem" according to Patrick. That means there isn't 1 solution to it and solving is needed.

Kangaroo is not precise enough for models going to be built, you're right on that. You can take a look at irregular sphere packing. They will give you a 3d voronoi, where each line has your desired lengths (sphere diameter):

Look at this software: http://math.lbl.gov/voro++

Best regards

Permalink Reply by Daniel Piker on November 11, 2013 at 12:18pm

I think there is some misunderstanding here.

Your issue is not with the accuracy of the solving, but with the choice of which lines you are setting as inputs to the springs.

If you input a consistent set of constraints Kangaroo will easily solve them precisely - 10 digit accuracy or more if you need it, and definitely way more than any manufacturing tolerances.

But when you set targets that conflict - for example, if you want to draw a square with side lengths of 10m and diagonals of 5m, there's just no way to do it - so the best you can do is minimize some total error.

I can see how just making all connections by proximity into springs will quickly introduce these sorts of conflicting constraints.

Something I'd suggest you could do here to get non conflicting constraints is make a sphere packing.

If you take a load of spheres of 4 of 5 different radii and pack them using springs with cutoffs, then draw lines between the centres of the spheres which are tangent, you will get 6 or 10 different lengths respectively.

Permalink Reply by Florian Frank on November 11, 2013 at 12:26pm

Hi daniel,

sorry for this. Reading through our posts it can be misundarstood, you're right. It's in fact the setup that leads to conflicts and not kangaroo. Thank you, for the correct explanation of the problem.

Didn't think about sphere packing with kangaroo though...i'll give it a try once ;-)

Have a nice day,

Permalink Reply by Daniel Piker on November 11, 2013 at 4:53pm

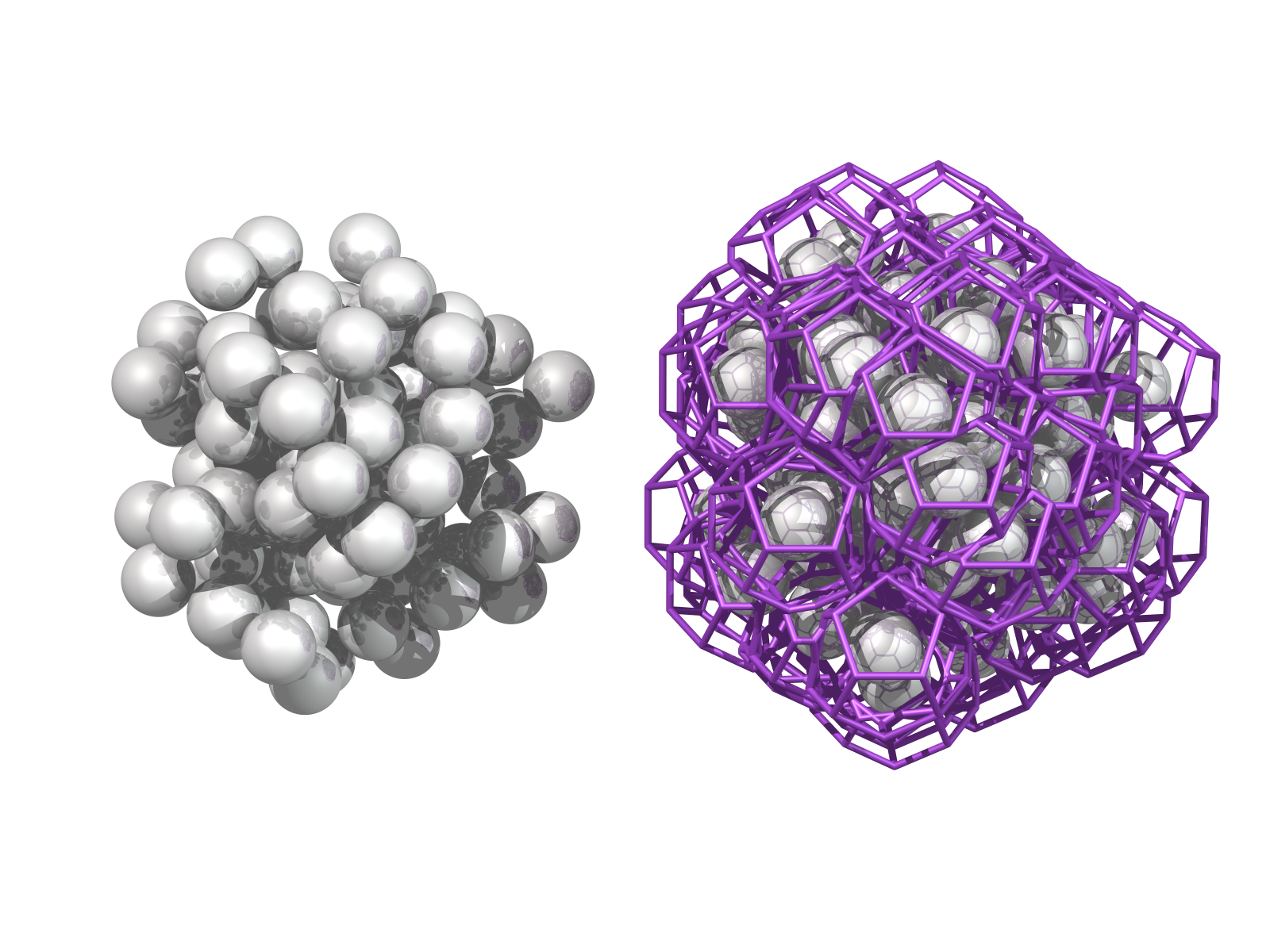
I made a quick test of sphere packing with radii of 5,6,7,8 or 9, using springs with cutoffs and attraction forces to pull them together so there are integer distances between ones which are tangent.

I stopped it when the accuracy was down to picometers, as I figure most manufacturing tolerances are a bit bigger than individual atoms ;)

Permalink Reply by oliver von Malm on November 12, 2013 at 3:19am

Hi Daniel, hi Florian,

Daniel, also from my side: Sorry for the misunderstanding. I did not mean at all to say that Kangaroo doesn't give precise results. How could I ;)? I use it frequently for various tasks and am very pleased to do so. I was guessing but couldn't properly explain that there are impossible solutions due to a given setup.

Still, was almost hoping that you would step in on this discussion :) the sphere packing looks great, was trying with spheres last night, but didn't get anywhere yet. Actually would you mind sharing the definition? Looks like it actually could solve the issue! Do you think it would even work with very large numbers of knots? Like 10000+? The stepping, is it imaginable with any value like i.e. 15 20, 35, 39, 60,...?

Thanks very much,

Oliver

Permalink Reply by Gogash on December 8, 2016 at 4:30am