Polygon center

by Jesus Galvez

Sep 22, 2013

Hello,

I don't know if this is intentional, but it sure is confusing. The [Polygon Center] component computes the center as the mean of all the vertices in a polygon. According to Wikipedia, it equals this:

The centroid of a finite set of {k} points \mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k in \mathbb{R}^n is

\mathbf{C} = \frac{\mathbf{x}_1+\mathbf{x}_2+\cdots+\mathbf{x}_k}{k}

However the center of a polygon by decomposition is this. 

The centroid of a plane figure X can be computed by dividing it into a finite number of simpler figures X_1,X_2,\dots,X_n, computing the centroid C_i and area A_i of each part, and then computing

C_x = \frac{\sum C_{i_x} A_i}{\sum A_i} , C_y = \frac{\sum C_{i_y} A_i}{\sum A_i}

Or this in general:

The centroid of a non-self-intersecting closed polygon defined by n vertices (x0,y0), (x1,y1), ..., (xn−1,yn−1) is the point (Cx, Cy), where 

C_{\mathrm x} = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)
C_{\mathrm y} = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)

and where A is the polygon's signed area,

A = \frac{1}{2}\sum_{i=0}^{n-1} (x_i\ y_{i+1} - x_{i+1}\ y_i)\;

Shouldn't the [Polygon Center] use this formula instead, or clarify that the "center" given is the mean?

EDIT: Sorry to have posted this in VB, C# and Python Coding. I meant to post it in Errors, Bugs and Oversights. 

  • up

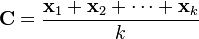
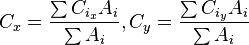
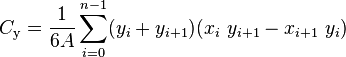
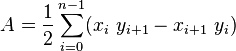
    Daniel Piker

    Just for triangles there are literally thousands of possible definitions for what is meant by the center.

    I'm not exaggerating - check out this encyclopedia of triangle centers !

    While there probably aren't quite so many that apply to general polygons, there are still a lot of possibilities :)

    1

    Sep 22, 2013

    • up

      David Rutten

      Polygon center computes two different centroids. Vertex average (which is admittedly a terrible way to define a center, as the shape of a polygon doesn't really matter much) and Edge average (which is a lot better and also the only result you actually see the preview of).

      I can certainly add more algorithms as long as they're quick to compute. Any suggestion (source or pseudo code please, no mathematical argle-bargle, can't read that) on which one you'd like to see?

      --

      David Rutten

      david@mcneel.com

      Tirol, Austria

      13

      Sep 22, 2013

      Load Previous Replies